RC既可以构成低通滤波电路,也可以构成高通滤波电路
1、高通滤波器
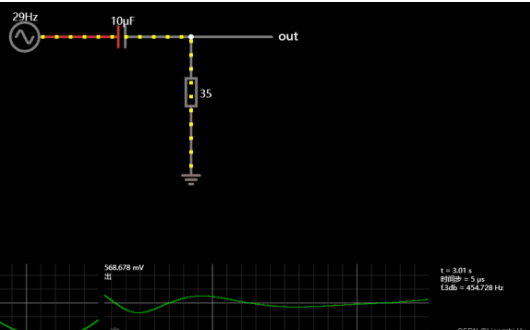
如果输入是个直流电压,ui电压的变化率为0,所以RL上没有电流通过,根据欧姆定律,即out=0V,电容完全”隔直“,也就是说频率为0的信号完全不可以通过隔直通交电路
频率较低的正弦信号,由于电流与电压的变化率线性正相关,所以RL上的电流很小,根据欧姆定律,所out的电压峰峰值也很小,也就是对低频信号衰减较大。如上图仿真,低频信号很难通过
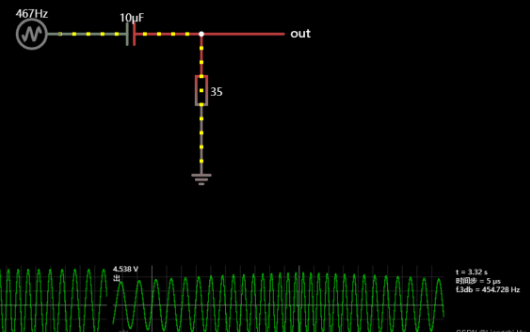
频率较高的正弦信号,电流因为ui电压变化率的增大而增大,out的峰峰值也随之增大,直到out峰峰值与ui峰峰值相等,即ui信号可以通过电容无损传递到out端。如上图仿真高频通过性好
所以,电容隔直通交电路体现的是一个高通滤波器性质
2、低通滤波器
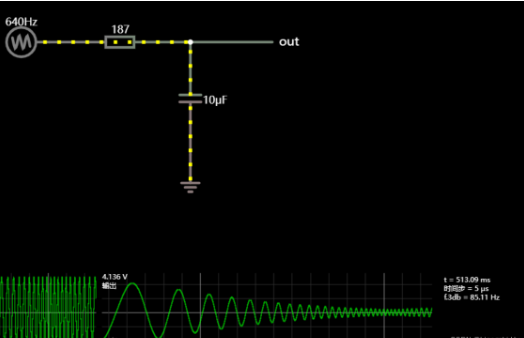
如果输入是个频率较低的正弦信号,虽然电容有“拖字诀”大法,但因为ui变化频率低,out还是能跟得上ui变化,也就是说低频的信号可以通过;
如果输入是个频率较高的正弦信号,电容的”拖字诀“效果明显,out不再跟得上ui的变化,out波形能够到达的峰值明显小于ui波形的峰值,也就是对高频信号衰减很大;
输入频率越高,out越跟不上ui变化,out波形的摆幅越小,即衰减越大。
所以,电容滤波电路体现的是一个低通滤波器性质。如上图仿真显示(频率逐渐增加)
rc滤波器截止频率计算:F(cutoff) =1 / (2πRC)。
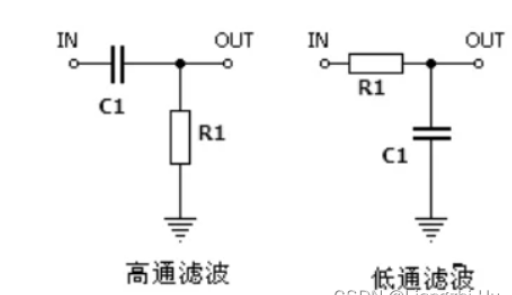
R、C的选取方式:
在计算后截止频率的情况下,R、C的取值可以成倍变化,如51Ω、22uF变为510Ω、2.2uF或5.1欧姆、220uF。为得到幅值衰减最小的波形,要保证:
1、滤波器的阻抗R1+Xc大于前级输入阻抗,越大越好。
2、滤波器的电容阻抗Xc远远小于后级输出阻抗RL2
————————————————
版权声明:本文为CSDN博主「Liangzhi.Hu」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/u010588566/article/details/127240900
