一、零输入响应和零状态响应
一阶电路就是电路中只含一个电容或者一个电感的电路。
此时求解电路电流时,要进行分解,将电路分成电阻网络和电感/电容。

分解后的电路还要对电容进行等效替换,变成没有电压的电容以及一个电压源。

很显然,根据叠加原理,电路中任意位置的电压,分别是输入电压(电源)和电容本身状态电压的叠加。如下图所示:

上图中(a)就是零状态响应,(b)就是零输入响应。这么做的一部分原因,将电容初值变为0,更利于求解微分方程;其次,求解电容两边的电压,指的是ab两点之间的电压,所两个电压(电源电压、状态电压)不能直接相加。
阶跃信号下,电容的零状态响应如下:
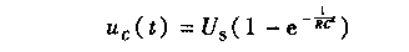
阶跃信号下,电容的零输入响应如下:
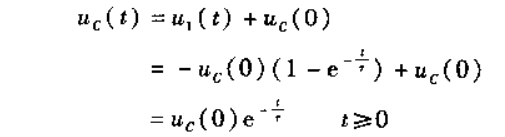
两者相加就是全响应。
二、三要素法
求解微分方程复杂且过分依赖数学方法。工程的方法在于总结、分析,得出更简便的理论和方法。
三要素法,就是总结阶跃信号下求全响应,就是求解三个关键值,如下所示:

三、瞬态和稳态
瞬态和稳态指的是:


直流电源作用下求解稳态响应和瞬态响应的方法如下所示:

正弦信号作用下的稳态响应和瞬态响应如下所示,其中稳态响应最终也会是同频率的正弦波


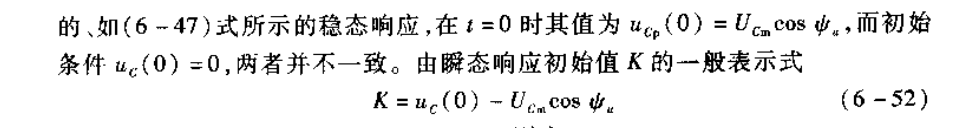
四、总结
求解一阶电路,有两种分解方法。一种是通过拓扑约束加上元件约束,求解微分方程,最后获得零输入响应和零状态响应;另一种是通过状态,全响应=瞬态响应+稳态响应。
————————————————
版权声明:本文为CSDN博主「木羽之灵」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/weixin_41605297/article/details/121061518
