一、 基本概念

1.1 基本概念

一个理想放大器的输出 y ( t ) y(t) y(t)是输入 x ( t ) x(t) x(t)的线性复制。真实情况下，在一个足够窄的范围，x变化很小，输出信号是叠加在偏置点上a0上的，a0可认为是工作（偏置）点，a1可认为是小信号增益，输入随输出变化时线性的因此把总的输出表示为：
y ( t ) ≈ a 0 + a 1 x ( t ) y ( t ) ≈ a _ { 0 } + a _ { 1 } x ( t ) y(t)≈a0​+a1​x(t)
输入信号幅度很大时，晶体管的偏置点受到很大的扰动，此时放大器的输入特性可用一个多项式来近似：
y ( t ) = a 0 + a 1 x ( t ) + a 2 x 2 ( t ) + ⋯ y ( t ) = a _ { 0 } + a _ { 1 } x ( t ) + a _ { 2 } x ^ { 2 } ( t ) + \cdots y(t)=a0​+a1​x(t)+a2​x2(t)+⋯

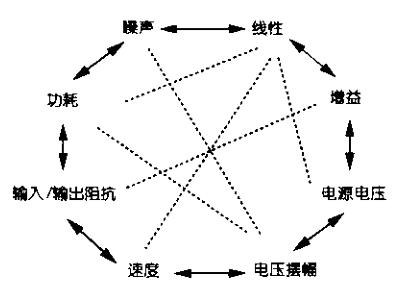
1.2 八边形法则

增益、速度、功耗、电源电压、线性度、噪声、输入输出阻抗、最大电压摆幅八种性能参数相互牵制，导致设计成为多维优化问题
在这里插入图片描述

1.3 两种分析方法

1.3.1 大信号分析

直流传输特性、直流偏置点分析

1.3.2 小信号分析

直流偏置点附近的小信号分析

二、共源极

2.1 电阻负载

电路结构
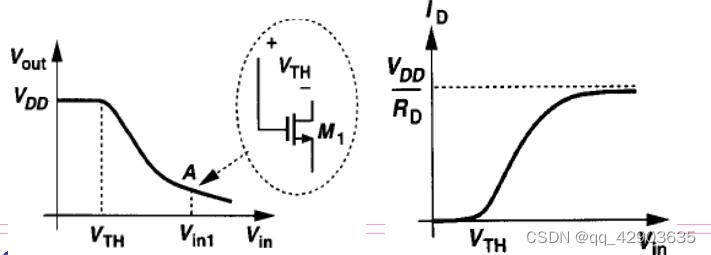
在这里插入图片描述

2.1.1 大信号分析

漏电流与输入电压的关系

I D = ( V D D − V o u t ) / R D I _ { D } = ( V _ { D D } – V _ { o u t } ) / R _ { D } ID​=(VDD​−Vout​)/RD​

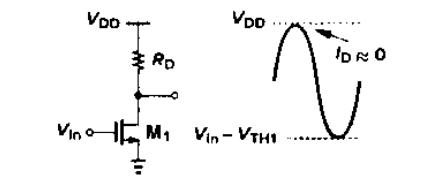
截止区 Vin<VTH：Vout=VDD，ID≈0
饱和区 Vin>VTH： V o u t = V D D − 1 2 u n C o x W L ( V i n − V T H ) 2 × R D V _ { o u t } = V _ { D D } – \frac { 1 } { 2 } u _ { n } C _ { o x} \frac { W } { L } ( V _ { i n } – V _ { T H } ) ^ { 2 } \times R _ { D } Vout​=VDD​−21​un​Cox​LW​(Vin​−VTH​)2×RD​
线性区Vin>VTH+Vout： V o u t = V D D − μ n C o x W L [ ( V i n − V T H ) V o u t − 1 2 V o u t 2 ] × R D V_{out}=V _ { D D } – μ _ { n } C _ { o x } \frac { W } { L } [ ( V _ { i n } – V _ { T H } ) V _ { out } – \frac { 1 } { 2 } V _ { out } ^ { 2 } ] \times R _ { D } Vout​=VDD​−μn​Cox​LW​[(Vin​−VTH​)Vout​−21​Vout2​]×RD​
深三极管区 V o u t < 2 ( V i n − V T H ) V _ { out } \lt 2 ( V _ { i n } – V _ { T H } ) Vout​<2(Vin​−VTH​)时，源漏之间的通道可以用一个线性电阻来表示 R o n = 1 u n C o x W L ( V G S − V T H ) R _ { o n } = \frac { 1 } { u _ { n } C _ { o x } \frac { W } { L } ( V _ { G S } – V _ { T H } ) } Ron​=un​Cox​LW​(VGS​−VTH​)1​
此时有 V o u t = V D D 1 + u n C o x W L ( V G S − V T H ) R D V _ { o u t} = \frac { V _ { D D } } { 1 + u _ { n } C _ { o x } \frac { W } { L } ( V _ { G S } – V _ { T H } ) R _ { D } } Vout​=1+un​Cox​LW​(VGS​−VTH​)RD​VDD​​
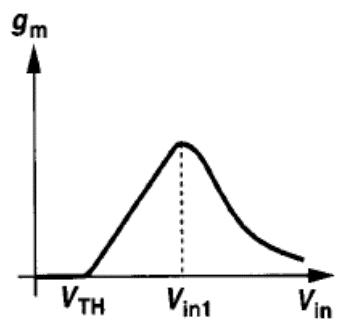
在这里插入图片描述

跨导与输入电压关系

饱和区： g m = ∂ I D ∂ V i n = u n C o x W L ( V i n − V T H ) g _ { m } = \frac { \partial I _ { D } } { \partial V _ { i n } } = u _ { n } C _ { o x } \frac { W } { L } ( V _ { i n } – V _ { T H } ) gm​=∂Vin​∂ID​​=un​Cox​LW​(Vin​−VTH​)
线性区： g m = ∂ I D ∂ V i n = μ n C o x W L V o u t g _ { m } = \frac { \partial I _ { D } } { \partial V _ { i n } } = μ_ { n } C _ { o x } \frac { W } { L } V _ { o u t } gm​=∂Vin​∂ID​​=μn​Cox​LW​Vout​
在这里插入图片描述

2.1.2 小信号分析

增益

V o u t = V D − R D × 1 2 μ n C o x W L ( V i n − V T H ) 2 V _ { o u t } = V _ { D } – R _ { D } \times \frac { 1 } { 2 } μ_ { n } C _ { o x } \frac { W } { L } ( V _ { i n } – V _ { TH} ) ^ { 2 } Vout​=VD​−RD​×21​μn​Cox​LW​(Vin​−VTH​)2 A v = ∂ V o u t ∂ V i n = − R D × μ n C o x ( V i n − V T H ) = − g m R D A _ { v } = \frac { \partial V _ { o u t } } { \partial V _ { i n } } = – R _ { D } \times μ _ { n } C _ { ox } ( V _ { i n } – V _ { T H } ) = – g _ { m } R _ { D } Av​=∂Vin​∂Vout​​=−RD​×μn​Cox​(Vin​−VTH​)=−gm​RD​

增益最大化

g m = − 2 μ n C o x W L I D g_{m}=- \sqrt{2 \mu _{n}C_{ox}\frac{W}{L}I_{D}} gm​=−2μn​Cox​LW​ID​
​，增益还可以写成
A v = − 2 μ n C o x W L I D V R D I D A _ { v } = – \sqrt { 2 μ _ { n} C _ { ox } \frac { W } { L } I _ { D }} \frac { V _ { RD } } { I _ { D } } Av​=−2μn​Cox​LW​ID​
​ID​VRD​​

  • 增大W/L，导致器件电容增大
  • 增大电阻RD上的电阻VRD，将限制最大摆幅
  • VRD不变，同时减小ID，则RD必须增大，会导致输出节点时间常数增大

2.1.3 输出摆幅

  • Vin刚好大于VTH时，输出电压接近VDD
  • Vin-VTH=Vout，M1处于线性区和饱和区边缘时，输出电压最小

在这里插入图片描述

2.1.4 考虑沟长调制效应的小信号分析

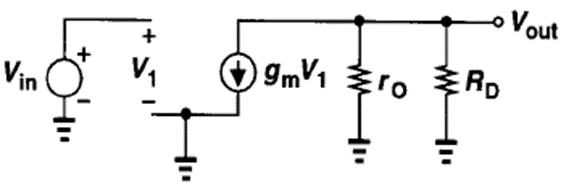
画出小信号电路图
在这里插入图片描述
V o u t = V D D − 1 2 u n C o x W L ( V i n − V T H ) 2 ( 1 + λ V o u t ) × R D V _ { o ut } = V _ { D D } – \frac { 1 } { 2 } u _ { n } C _ { o x } \frac { W } { L } ( V _ { i n } – V _ { T H } ) ^ { 2 } ( 1 + λ V _ { o u t } ) \times R _ { D } Vout​=VDD​−21​un​Cox​LW​(Vin​−VTH​)2(1+λVout​)×RD​
对Vin求偏导有
A v = − g m ( R D / / r o ) A _ { v } = – g _ { m } ( R _ { D } // r_ { o } ) Av​=−gm​(RD​//ro​)
或者由KCL求解方程同样可得增益
g m V i n + V o u t ( R D / / r o ) = 0 g _ { m } V _ { i n } + \frac { V _ { o u t } } { ( R _ { D } // r_ { o } ) } = 0 gm​Vin​+(RD​//ro​)Vout​​=0 当负载电阻非常大时（负载为电流源）
A v = − g m ( R D / / r o ) ≈ − g m r 0 A _ { v } = – g _ { m } ( R _ { D } / /r _ { o } ) ≈- g _ { m } r _ { 0 } Av​=−gm​(RD​//ro​)≈−gm​r0​ gmro称为晶体管的本征增益，代表用单个器件能够得到的最大电压增益

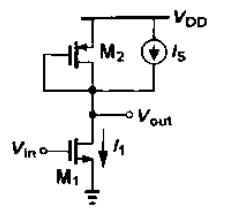
2.2 二极管型负载

2.2.1 大信号特性

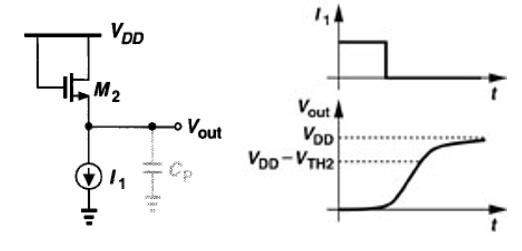
  • 在I1减小的同时，M2的过驱动电压也减小。当I1小到有VGS≈VTH2时，Vout≈VDD-VTH2
  • 实际上，如果IDD接近于零时，M2的亚阈值电导最终会使Vout=VDD。但电流很小时，输出节点处有限的电容会减缓从VDD-VTH2到VDD的变化
  • 具有频繁开关动作的电路中，当电流IDD降到很小时，，Vout保持在VDD-VTH2附近
    在这里插入图片描述

2.2.2 小信号分析

二极管负载等效电阻

不考虑体效应时
V x I x = ( 1 / g m ) / / r o ≈ 1 / g m \frac { V _ { x } } { I _ { x } } =(1/g_{m})//r_{o}\approx 1/g_{m} Ix​Vx​​=(1/gm​)//ro​≈1/gm​ 考虑体效应时
V x I x = 1 g m + g m b / / r o ≈ 1 g m + g m b \frac { V _ { x } } { I _ { x } } = \frac { 1 } { g _ { m } + g _ { m b } } // r_ { o } \approx \frac { 1 } { g _ { m } + g _ { m b } } Ix​Vx​​=gm​+gmb​1​//ro​≈gm​+gmb​1​

增益

A v = − g m 1 R D = − g m 1 g m 2 + g m b 2 = − g m 1 g m 2 1 1 + η A _ { v } = – g _ { m1 } R _ { D } = – \frac { g _ { m1 } } { g _ { m 2 } + g _ { m b 2 } } = – \frac { g _ { m 1 } } { g _ { m 2 } } \frac { 1 } { 1+η } Av​=−gm1​RD​=−gm2​+gmb2​gm1​​=−gm2​gm1​​1+η1​ 其中， η = g m b 2 / g m 2 = ∂ V T H ∂ V S B η = g _ { m b 2 } / g _ { m 2 }= \frac { \partial V _ { TH } } { \partial V _ { SB } } η=gmb2​/gm2​=∂VSB​∂VTH​​
又有跨导 g m = 2 I D μ n C o x W / L g _ { m } = \sqrt { 2 I _ { D } μ_{n} C _ { o x } W / L } gm​=2ID​μn​Cox​W/L
​，代入上式有：
A v = − ( W / L ) 1 ( W / L ) 2 1 1 + η A_{v}=- \frac{\sqrt{(W/L)_{1}}}{\sqrt{(W/L)_{2}}}\frac{1}{1+ \eta} Av​=−(W/L)2​
​(W/L)1​
​​1+η1​
同样的，对PMOS二极管负载，由于没有体效应，所以有增益：
A v = − u n ( W / L ) 1 u p ( W / L ) 2 = − g m 1 g m 2 A _ { v } = – \frac { \sqrt { u _ { n } ( W / L ) _ { 1 } } } { \sqrt { u _ { p } ( W / L ) _ { 2 } } }=- \frac { g _ { m 1 } } { g _ { m 2 } } Av​=−up​(W/L)2​
​un​(W/L)1​
​​=−gm2​gm1​​

增大增益
  • 二极管连接负载共源极的增益是器件尺寸的弱函数，高增益会造成晶体管的宽度或沟道长度过大而不均衡
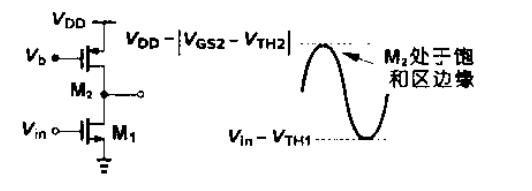
  • 允许的输出摆幅减小,如下图
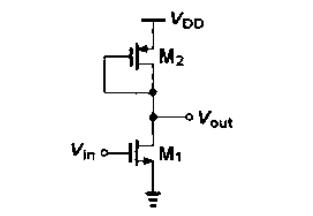
    在这里插入图片描述

u n ( W L ) 1 ( V G S 1 − V T H 1 ) 2 ≈ μ p ( W L ) 2 ( V G S 2 − V T H 2 ) 2 u _ { n } ( \frac { W } { L } )_{1} ( V _ { G S 1 } – V _ { T H 1 } ) ^ { 2 } \approx μ _ { p } ( \frac { W } { L } ) _ { 2 } ( V _ { GS 2 } – V _ { T H 2 } ) ^ { 2 } un​(LW​)1​(VGS1​−VTH1​)2≈μp​(LW​)2​(VGS2​−VTH2​)2 A v = ∣ V G S 2 − V T H 2 ∣ V G S 1 − V T H 1 = V D D − V o u t − ∣ V T H 2 ∣ V i n − V T H 1 A _ { v } = \frac { | V _ { G S2 } – V _ { T H 2 } | } { V _ { G S 1 } – V _ { T H 1 } } = \frac { V _ { D D } – V _ { o u t } – |V _ { T H 2 } | } { V _ { i n } – V _ { T H 1 } } Av​=VGS1​−VTH1​∣VGS2​−VTH2​∣​=Vin​−VTH1​VDD​−Vout​−∣VTH2​∣​ 若μn=2μp，要达到10倍增益，M1的过驱动电压为200mV，|VTH2|=0.7V，则|VGS2|=2.7V，因为Vout,min=VDD-|VGS2|，所以最小输出电压上升，即输出摆幅下降

2.2.3 输出摆幅(负载为PMOS)

  • 保证M1和M2都工作在饱和区时的输出范围，对M2满足VGS2>VTH2，对M1满足Vout>Vin-VTH1
  • Vout,min = VDD – |VGS2|，此时IDD处于饱和电流与线性电流分界点，VGS2最大
  • Vout,max=VDD – |VTH2|，此时IDD比较小，M2刚好导通且处于饱和状态

2.2.4 增大摆幅

如下图，M1工作在饱和区，漏电流为I1，在电路上增加一个电流源IS=0.75I1
在这里插入图片描述
A v ≈ − g m 1 g m 2 = − 4 u n ( W / L ) 1 u p ( W / L ) 2 A_{v}≈- \frac { g _ { m 1 } } { g _ { m 2 } }=- \sqrt { \frac { 4 u _ { n } ( W / L ) _ { 1 } } { u _ { p } ( W / L ) _ { 2 } } } Av​≈−gm2​gm1​​=−up​(W/L)2​4un​(W/L)1​​
​ 同时， μ n ( W L ) ( V G S 1 − V T H 1 ) 2 ≈ 4 μ p ( W L ) 2 ( V G S 2 − V T H 2 ) 2 μ _ { n } ( \frac { W } { L } ) ( V _ { G S 1 } – V _ { T H 1 } ) ^ { 2 } \approx 4 μ _ { p } ( \frac { W } { L } ) _ { 2 } ( V _ { G S 2 } – V _ { T H 2 } ) ^ { 2 } μn​(LW​)(VGS1​−VTH1​)2≈4μp​(LW​)2​(VGS2​−VTH2​)2 A v ≈ − 4 ∣ V G S 2 − V T H 2 ∣ V G S 1 − V T H 1 A _ { v } \approx – \frac { 4 | V _ { G S 2 } – V _ { T H 2 } | } { V _ { G S 1 } – V _ { T H 1 } } Av​≈−VGS1​−VTH1​4∣VGS2​−VTH2​∣​ 上式说明，同样要达到10倍增益，M1的过驱动电压为200mV，|VTH2|=0.7V的情况下，|VGS2|=1.2V，相比没加电流源时|VGS2|=2.7V，使输出最低电压下降，增大了摆幅

2.3 电流源负载

对于电阻或者二极管连接的负载而言，增大阻值会消耗直流压降，从而限制输出电压的摆幅，用不服从欧姆定律的电流源来替代负载
A v = − g m 1 R o u t = − g m 1 ( r o 1 / / r o 2 ) A _ { v } = – g _ { m 1 } R _ { o u t } = – g _ { m 1 } ( r _ { o 1 } // r_ { o 2 } ) Av​=−gm1​Rout​=−gm1​(ro1​//ro2​)
在这里插入图片描述
A v = − 2 u n C o x W L I D 1 ( λ 1 + λ 2 ) I D A _ { v } = – \sqrt { 2 u _ { n } C _ { ox } \frac { W } { L } I _ { D } } \frac { 1 } { ( λ _ { 1 } + λ _ { 2 } ) I _ { D } } Av​=−2un​Cox​LW​ID​
​(λ1​+λ2​)ID​1​
λ∝1/L，通过简单地增加M2的沟道长度，就可以使 ∣ V D S 2 , m i n ∣ = ∣ V G S 2 − V T H 2 ∣ | V _ { DS 2,min } | = | V _ { GS2 } – V _ { T H 2 } | ∣VDS2,min​∣=∣VGS2​−VTH2​∣减小，但是会在M2的输出节点引入大电容

2.4 工作在线性区的NMOS负载

该电路使M2栅压偏置在足够低的电平，保证M2全部输出电压摆幅范围内工作在深线性区
R o n 2 = 1 μ p C o x ( W / L ) 2 ( V D D − V b − ∣ V T H P ∣ ) R _ { o n 2 } = \frac { 1 } { μ_ { p } C _ { o x } ( W / L ) _ { 2 } ( V _ { D D } – V _ { b } – | V _ { TH P } |) } Ron2​=μp​Cox​(W/L)2​(VDD​−Vb​−∣VTHP​∣)1​
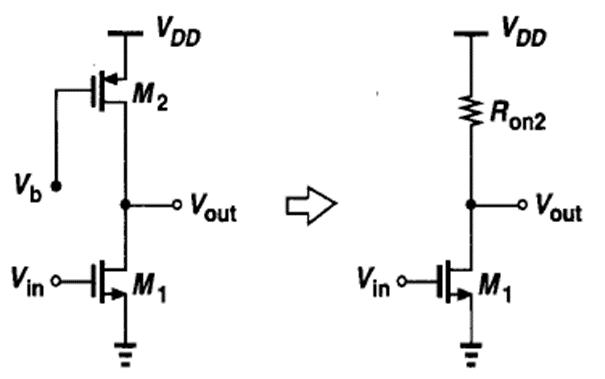
在这里插入图片描述
A v = − g m R o n 2 A _ { v } = – g _ { m } R _ { o n 2 } Av​=−gm​Ron2​ 输出电压摆幅和电阻负载共源极相同。该电路的等效电阻Ron2受到很多参数影响，这些参数随工艺和温度的改变而改变，且提供一个精确地Vb需增加电路的复杂性

2.5 带源极负反馈的共源极

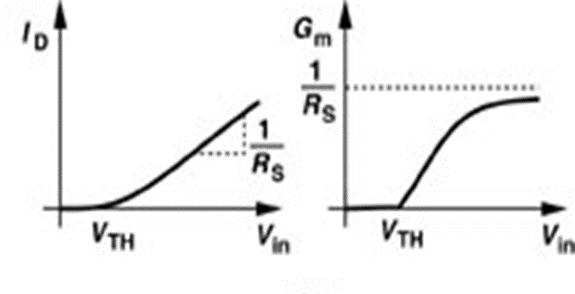
漏电流与过驱动电压之间的非线性关系引入大量非线性（gm），通过在晶体管的源端串联一个“负反馈”电阻，以使输入器件更加线性。

2.5.1 大信号分析

等效跨导

定义一个等效跨导 G m = ∂ I D ∂ V i n G_{m}= \frac{\partial I_{D}}{\partial V_{in}} Gm​=∂Vin​∂ID​​，其中 V i n = V G S 1 + I D R S V _ { i n } = V _ { G S 1 } + I _ { D } R _ { S } Vin​=VGS1​+ID​RS​，此时有，
G m = ∂ I D ∂ V i n = ∂ I D ∂ V G S 1 ∂ V G S 1 ∂ V i n = g m ∂ V G S 1 ∂ V i n = g m 1 + g m R s G_{m}= \frac{\partial I_{D}}{\partial V_{in}}= \frac{\partial I_{D}}{\partial V_{GS1}}\frac{\partial V_{GS1}}{\partial V_{in}}=g_{m}\frac{\partial V_{GS1}}{\partial V_{in}}= \frac{g_{m}}{1+g_{m}R_{s}} Gm​=∂Vin​∂ID​​=∂VGS1​∂ID​​∂Vin​∂VGS1​​=gm​∂Vin​∂VGS1​​=1+gm​Rs​gm​​ A v = − g m R D 1 + g m R s A _ { v } = – \frac { g _ { m } R _ { D } } { 1 + g _ { m } R _ { s } } Av​=−1+gm​Rs​gm​RD​​ 如果Rs>>1/gm，则Gm≈1/Rs

  • 增加源极负反馈电阻，使增益是gm的弱函数，提高了线性特性
  • 线性化的获得是以牺牲增益为代价的
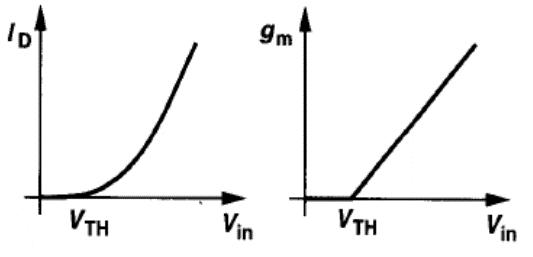
大信号特性

Rs=0
饱和区时：
g m = μ n C o x W L ( V i n − V T H ) g _ { m } = μ_ { n } C _ { o x } \frac { W } { L } ( V _ { i n } – V _ { T H } ) gm​=μn​Cox​LW​(Vin​−VTH​) I D = 1 2 μ n C o x W L ( V i n − V T H ) 2 I _ { D } = \frac { 1 } { 2 } μ _ { n } C _ { o x } \frac { W } { L } ( V _ { i n } – V _ { T H } ) ^ { 2 } ID​=21​μn​Cox​LW​(Vin​−VTH​)2
在这里插入图片描述

Rs≠0

  • Vin很小，M1导通时 1 / g m > R s 1 / g _ { m } \gt R _ { s } 1/gm​>Rs​，Gm≈gm
  • Vin增加时， G m = g m 1 + g m R s G _ { m } = \frac { g _ { m } } { 1 + g _ { m } R _ { s } } Gm​=1+gm​Rs​gm​​
  • Vin很大时，Rs>>1/gm，Gm=1/Rs
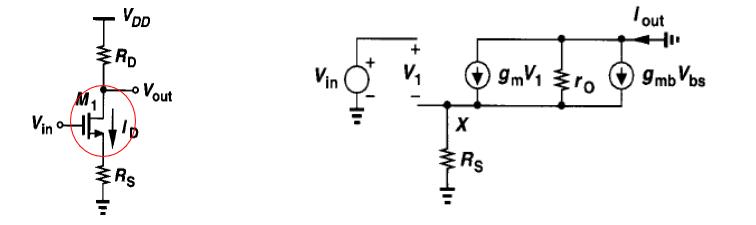
    在这里插入图片描述

2.5.1小信号分析

辅助定理：在线性电路中，电压增益等于-GmRout，其中-Gm表示输出与地短接时电路的跨导；Rout表示当输入电压为零时电路的输出电阻
1.求Gm：直流电压源短路，直流电流源开路；输入端为Vin，输出端接地，电流为Iout；Gm=Iout/Vin
2.求Rout：直流电压源短路，直流电流源开路；输入接地；输出为Vx，Ix，Rout=Vx/Ix

等效跨导与输出电阻

I o u t = g m V 1 − V X r o + g m b V b s = g m ( V i n − I o u t R s ) − I o u t R s r o − g m b I o u t R s I_{out}=g_{m}V_{1}- \frac{V_{X}}{r_{o}}+g_{mb}V_{bs}=g_{m}(V_{in}-I_{out}R_{s})- \frac{I_{out}R_{s}}{r_{o}}-g_{mb}I_{out}R_{s} Iout​=gm​V1​−ro​VX​​+gmb​Vbs​=gm​(Vin​−Iout​Rs​)−ro​Iout​Rs​​−gmb​Iout​Rs​ G m = I o u t V i n = g m r o R s + [ 1 + ( g m + g m b ) R s ] r o G_{m}= \frac{I_{out}}{V_{in}}= \frac{g_{m}r_{o}}{R_{s}+ \left[ 1+(g_{m}+g_{mb})R_{s}\right] r_{o}} Gm​=Vin​Iout​​=Rs​+[1+(gm​+gmb​)Rs​]ro​gm​ro​​
在这里插入图片描述
V X = [ I x + ( g m + g m b ) R s I x ] r o + I x R s V_{X}= \left[ I_{x}+(g_{m}+g_{mb})R_{s}I_{x}\right] r_{o}+I_{x}R_{s} VX​=[Ix​+(gm​+gmb​)Rs​Ix​]ro​+Ix​Rs​ R o u t = V X I X = [ 1 + ( g m + g m b ) R s ] r o + R s = [ 1 + ( g m + g m b ) r o ] R s + r o R_{out}= \frac{V_{X}}{I_{X}}= \left[ 1+(g_{m}+g_{mb})R_{s}\right] r_{o}+R_{s}= \left[ 1+(g_{m}+g_{mb})r_{o}\right] R_{s}+r_{o} Rout​=IX​VX​​=[1+(gm​+gmb​)Rs​]ro​+Rs​=[1+(gm​+gmb​)ro​]Rs​+ro​ 一般 ( g m + g m b ) r 0 > > 1 ( g _ { m } + g _ { m b } ) r _ { 0 } >>1 (gm​+gmb​)r0​>>1， R o u t ≈ [ 1 + ( g m + g m b ) R s ] r 0 R _ { o u t } \approx [ 1 + ( g _ { m } + g _ { m b } ) R _ { s } ] r _ { 0 } Rout​≈[1+(gm​+gmb​)Rs​]r0​
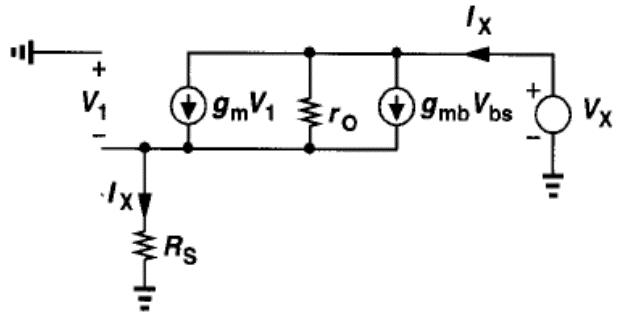
在这里插入图片描述

增益

Rout很大，与RD并联后被忽略
A v = − g m R D ( g m + g m b ) R s + 1 ≈ − g m R D g m R s + 1 A _ { v } = – \frac { g _ { m } R _ { D } } { ( g _ { m } + g _ { m b } ) R _ { s } + 1 } \approx – \frac { g _ { m } R _ { D } } { g _ { m } R _ { s } + 1 } Av​=−(gm​+gmb​)Rs​+1gm​RD​​≈−gm​Rs​+1gm​RD​​

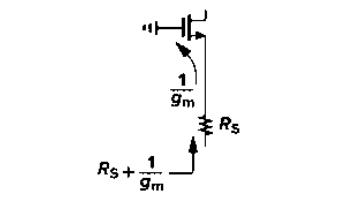
计算增益的等效方法

A v = − g m R D 1 + g m R S = − R D 1 / g m + R s A _ { v } = – \frac { g _ { m } R _ { D } } { 1 + g _ { m } R _ { S } } = – \frac { R _ { D } } { 1 / g _ { m } + R _ { s } } Av​=−1+gm​RS​gm​RD​​=−1/gm​+Rs​RD​​

  • 分母称为“在源极通路上看到的电阻”，其等于MOS器件跨导的倒数与明确的从源端看到的与地之间的电阻的串联
  • 增益为从漏极结点看到的电阻除以源极通路上的总电阻
    在这里插入图片描述

三、源跟随器（共漏极）

共源极放大器在给定电源电压下，要获得更高的电压增益，负载阻抗必须尽可能大。由于负载电阻与输出电阻是并联关系，小的负载电阻会影响整个输出阻抗，进而导致增益下降，所以这时要在放大器后面放置一个“缓冲器”，源跟随器就起这样一个缓冲作用。
源跟随器在提高输出阻抗的同时，在栅极接收信号，在源极驱动负载，使源极电势能“跟随”栅压

3.1 大信号分析

  • Vin<VTH时，M1处于截止状态，Vout等于0
  • Vin增大并超过VTH，M1导通进入饱和区
  • Vin进一步增大，Vout跟随Vin变化，且二者之差为VGS
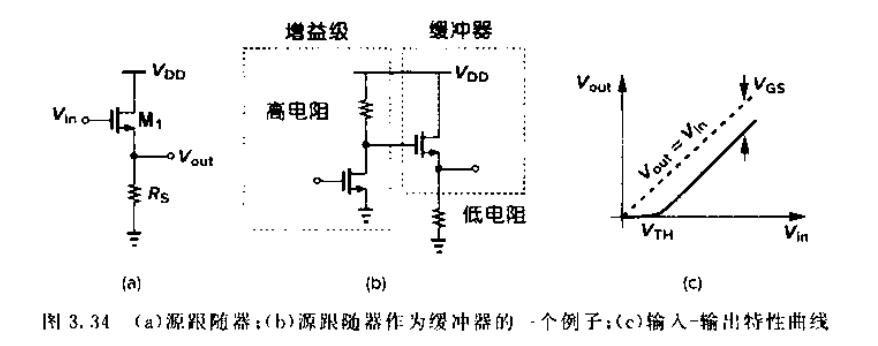
    在这里插入图片描述

1 2 u n C o x W L ( V i n − V o u t − V T H ) 2 R S = V o u t \frac { 1 } { 2 } u _ { n } C _ { o x } \frac { W } { L } ( V _ { i n } – V _ { out } – V _ { T H } ) ^ { 2 } R _ { S } = V _ { out } 21​un​Cox​LW​(Vin​−Vout​−VTH​)2RS​=Vout​ 将 g m = μ n C o x W L ( V i n − V o u t − V T H ) g _ { m } = μ _ { n } C _ { o x } \frac { W } { L } ( V _ { i n } – V _ { out } – V _ { T H } ) gm​=μn​Cox​LW​(Vin​−Vout​−VTH​)代入上式，并对Vin求导，其中 η = ∂ V o u t ∂ V i n η=\frac{\partial V_{out}}{\partial V_{in}} η=∂Vin​∂Vout​​：
A v = g m R s 1 + ( g m + g m b ) R s A _ { v } = \frac { g _ { m } R _ { s } } { 1 + ( g _ { m } + g _ { m b } ) R _ { s } } Av​=1+(gm​+gmb​)Rs​gm​Rs​​

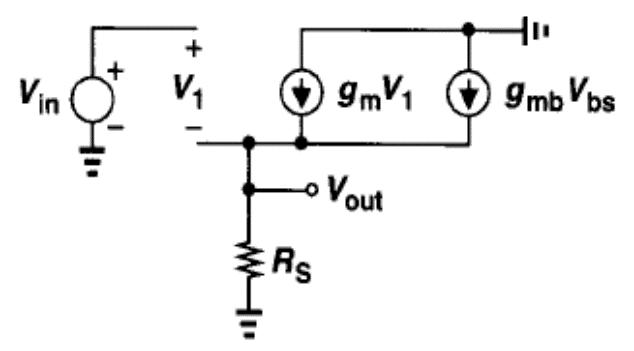
3.2 小信号分析

增益

画出源跟随器小信号电路，很明显要考虑体效应，由KCL得： g m V 1 − g m b V o u t = V o u t R s g _ { m } V _ { 1 } – g _ { m b } V _ { o u t } = \frac { V _ { o u t } } { R _ { s } } gm​V1​−gmb​Vout​=Rs​Vout​​ A v = V o u t V i n = g m R s 1 + ( g m + g m b ) R s A_{v}= \frac{V_{out}}{V_{in}}= \frac{g_{m}R_{s}}{1+(g_{m}+g_{mb})R_{s}} Av​=Vin​Vout​​=1+(gm​+gmb​)Rs​gm​Rs​​
在这里插入图片描述

  • 增益<1
  • 当Vin≈VTH时，增益从零开始单调增加（gm随Vin线性增加）
  • 随gm变大，A接近gm/(gm+gmb) = 1/(1+η)随Vout增大而缓慢减少，所以Av趋近1

输出电阻

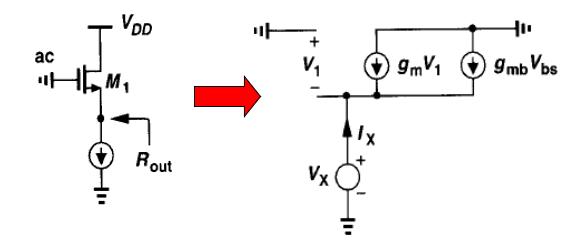
在这里插入图片描述
由KCL得： I X − g m V X − g m b V X = 0 I _ { X } – g _ { m } V _ { X } – g _ { m b } V _ { X } = 0 IX​−gm​VX​−gmb​VX​=0 R o u t = 1 g m + g m b R _ { o u t } = \frac { 1 } { g _ { m } + g _ { m b } } Rout​=gm​+gmb​1​

四、共栅极

4.1 大信号分析

饱和区 V o u t = V D D − 1 2 μ n C o x W L ( V b − V i n − V T H ) 2 R D V _ { o u t } = V _ { D D } – \frac { 1 } { 2 } μ _ { n } C _ { ox } \frac { W } { L } ( V _ { b } – V _ { in } – V _ { TH } ) ^ { 2 } R _ { D } Vout​=VDD​−21​μn​Cox​LW​(Vb​−Vin​−VTH​)2RD​ 对Vin求偏导有
A v = ∂ V o u t ∂ V i n = μ n C o x W L ( V b − V i n − V T H ) R D ( 1 + η ) = g m ( 1 + η ) R D A_{v}= \frac{\partial V_{out}}{\partial V_{in}}= \mu _{n}C_{ox}\frac{W}{L}(V_{b}-V_{in}-V_{TH})R_{D}(1+ \eta)=g_{m}(1+ \eta)R_{D} Av​=∂Vin​∂Vout​​=μn​Cox​LW​(Vb​−Vin​−VTH​)RD​(1+η)=gm​(1+η)RD​

  • 增益是正值
  • 体效应使增益相对共源极变大了

4.2 小信号分析

增益

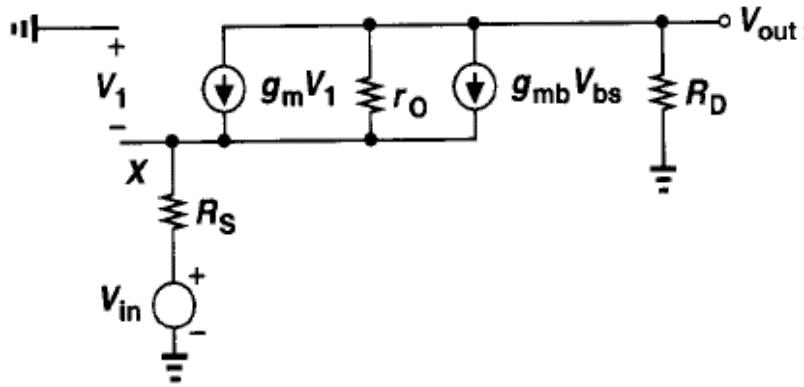
在这里插入图片描述
写出X节点和输出节点的的KVL方程，整理后得
A v = V o u t V i n = ( g m + g m b ) r o + 1 r o + ( g m + g m b ) r o R s + R s + R D R D A _ { v } = \frac { V _ { o u t } } { V _ { i n } } = \frac { ( g _ { m } + g _ { m b } ) r _ { o } + 1 } { r_ { o } + ( g _ { m } + g _ { m b } ) r _ { o } R _ { s } + R _ { s } + R _ { D } }R_{D} Av​=Vin​Vout​​=ro​+(gm​+gmb​)ro​Rs​+Rs​+RD​(gm​+gmb​)ro​+1​RD​
当Rs=0，ro>>RD及gmro>>1时 A v ≈ ( g m + g m b ) r o r o R D = ( g m + g m b ) R D = g m ( 1 + η ) R D A _ { v } \approx \frac { ( g _ { m } + g _ { m b } ) r _ { o} } { r _ { o } } R _ { D } = ( g _ { m } + g _ { m b } ) R _ { D } = g _ { m } ( 1 + η ) R _ { D } Av​≈ro​(gm​+gmb​)ro​​RD​=(gm​+gmb​)RD​=gm​(1+η)RD​

输入电阻

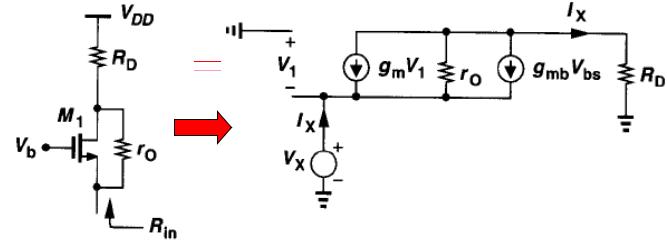
在这里插入图片描述
R D I X + r o [ I X − ( g m + g m b ) V X ] = V X R _ { D } I _ { X } + r _ { o } [ I _ { X } – ( g _ { m } + g _ { m b } ) V _ { X } ] = V _ { X } RD​IX​+ro​[IX​−(gm​+gmb​)VX​]=VX​ R i n = V X I X = R D + r o 1 + ( g m + g m b ) r o R _ { i n } = \frac { V _ { X } } { I _ { X } } = \frac { R _ { D } + r _ { o } } { 1 + ( g _ { m } + g _ { m b } ) r _ { o } } Rin​=IX​VX​​=1+(gm​+gmb​)ro​RD​+ro​​ 若 ( g m + g m b ) r 0 > > 1 ( g _ { m } + g _ { m b } ) r _ { 0 } >> 1 (gm​+gmb​)r0​>>1，则有 R i n ≈ R D ( g m + g m b ) r o + 1 ( g m + g m b ) R _ { i n } \approx \frac { R _ { D } } { ( g _ { m } + g _ { m b } ) r _ { o } } + \frac { 1 } { ( g _ { m } + g _ { m b } ) } Rin​≈(gm​+gmb​)ro​RD​​+(gm​+gmb​)1​

  • 当RD=0时，所得输入电阻结果与源跟随器在源端看到的输出电阻结果一致。因为RD=0时，电路结构和源跟随器是一样的
  • 当RD趋近于无穷大（负载为电流源）时，输入阻抗也趋近于无穷，此时共栅极源极输入小信号趋近于Vin，所以可以看出其增益 A v = ( g m + g m b ) r 0 + 1 A _ { v } = ( g _ { m } + g _ { m b } ) r _ { 0 } + 1 Av​=(gm​+gmb​)r0​+1与源极是否接“反馈电阻”无关

输出电阻

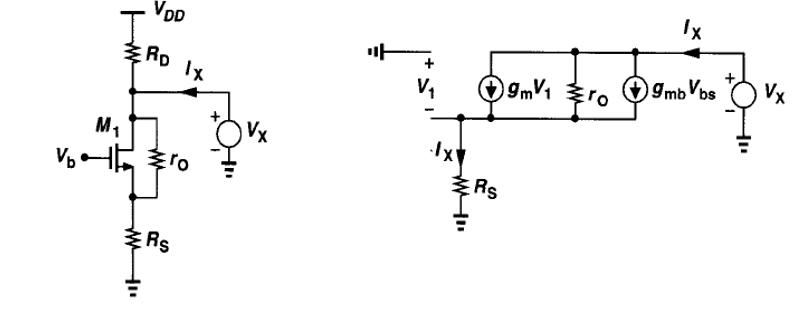
在这里插入图片描述
将图中等效电阻值代入共源极负反馈电路的输出电阻表达式中有： R o u t = { [ 1 + ( g m + g m b ) r o ] R s + r o } / / R D R _ { o u t } = \{ [ 1 + ( g _ { m } + g _ { m b } ) r _ { o } ] R _ { s } + r _ { o } \} / / R _ { D } Rout​={[1+(gm​+gmb​)ro​]Rs​+ro​}//RD​

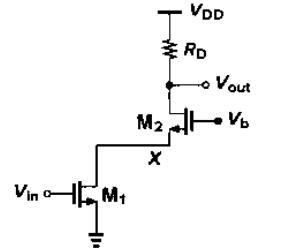
五、共源共栅级

共栅极的输入信号可以是电流（例3.17），共源极中的晶体管可以将电压信号转化为电流信号。共源极和共栅极的级联叫做共源共栅结构（cascode）。
如下图，M1产生与输入电压Vin成正比的小信号漏电流，M2仅仅是使电流流经RD。M1被称为输入器件，M2被称为共源共栅器件。
共源共栅
偏置条件
M1： V b − V G S 2 > ( V i n − V T H 1 ) V _ { b }- V _ { G S 2 } \gt ( V _ { i n } – V _ { T H 1 } ) Vb​−VGS2​>(Vin​−VTH1​)
M2： V o u t ≥ V i n − V T H 1 + V G S 2 − V T H 2 V _ { o u t } \geq V _ { i n } – V _ { T H 1 } + V _ { G S 2 } – V _ { T H 2 } Vout​≥Vin​−VTH1​+VGS2​−VTH2​

5.1 小信号分析

5.1.1 增益

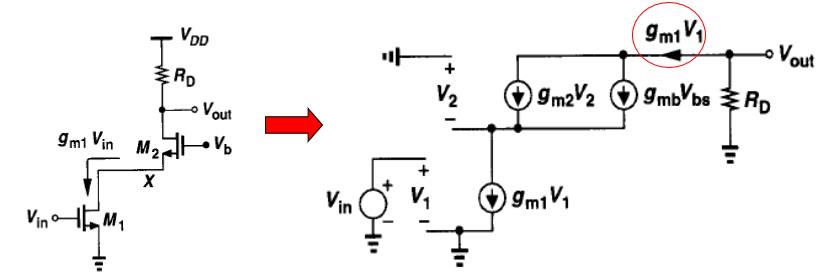
在这里插入图片描述
M1和M2都工作在饱和区。若λ=0，由输入管M1产生的漏电流必定流过共源共栅器件M2，且VIn=V1，因此 A v = V o u t / V i n = − g m 1 V 1 R D / V i n = − g m 1 R D A _ { v } = V _ { o u t } / V _ { i n } =- g _ { m 1 } V _ { 1 } R _ { D } / V _ { i n } =- g _ { m 1 } R _ { D } Av​=Vout​/Vin​=−gm1​V1​RD​/Vin​=−gm1​RD​ 若忽略沟道长度调制效应，共源共栅放大器与共源放大器具有相同的电压增益

5.1.2 增益（不考虑RD时）

电路可以看成带负反馈电阻ro1的共源极，因此输出电阻为 R o u t = r o 2 + [ 1 + ( g m 2 + g m b 2 ) r 02 ] r o 1 R_ { out } = r _ { o 2 } + [ 1 + ( g _ { m 2 } + g _ { m b 2 } ) r _ { 02 } ] r _ { o 1 } Rout​=ro2​+[1+(gm2​+gmb2​)r02​]ro1​ 若 g m 2 r o 2 > > 1 g _ { m 2 } r _ { o 2 } >> 1 gm2​ro2​>>1，则 R o u t ≈ ( g m 2 + g m b 2 ) r 02 r 01 R_ { o u t } \approx ( g _ { m 2 } + g _ { m b 2 } ) r _ { 02 } r _ { 01 } Rout​≈(gm2​+gmb2​)r02​r01​ 输出电阻提高了 ( g m 2 + g m b 2 ) r 02 ( g _ { m 2 } + g _ { m b 2 } ) r _ { 02 } (gm2​+gmb2​)r02​倍
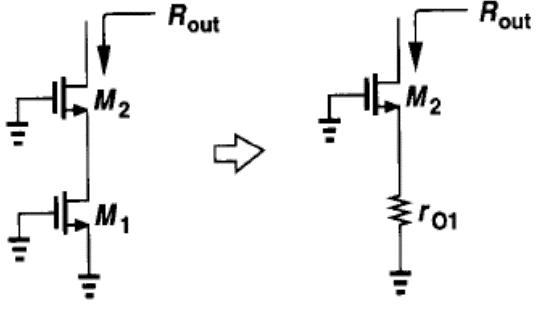
在这里插入图片描述

因为M1的漏电流必定流过M2，跨导与共源极相同Gm=gm
A v = − G m r o u t ≈ − g m 1 ( g m 2 + g m b 2 ) r 02 r 01 ≈ − ( g m 1 r 01 ) 2 A _ { v } = – G _ { m } r _ { out} \approx -g _ { m 1 } (g _ { m 2 } + g _ { m b 2 } ) r _ { 02 } r _ { 01 } \approx -( g _ { m1 } r _ { 01 } ) ^ { 2 } Av​=−Gm​rout​≈−gm1​(gm2​+gmb2​)r02​r01​≈−(gm1​r01​)2

5.1.3 提高增益的方法（相对共源极）

采用共源共栅
A v ≈ − ( g m r 0 ) 2 A _ { v } \approx -( g _ { m } r _ { 0 } ) ^ { 2 } Av​≈−(gm​r0​)2 增益增大gmro倍，同时过驱动电压增加一倍，输出摆幅下降
提高共源极输入器件的长度
A v = − g m r o = − μ n C o x W L I D 1 λ I D A_{v}=-g_{m}r_{o}= -\sqrt{\mu _{n}C_{ox}\frac{W}{L}I_{D}}\frac{1}{\lambda I_{D}} Av​=−gm​ro​=−μn​Cox​LW​ID​
​λID​1​ λ∝1/L，Av∝ L \sqrt{L} L
​，L增大n倍，Av增大n/2倍
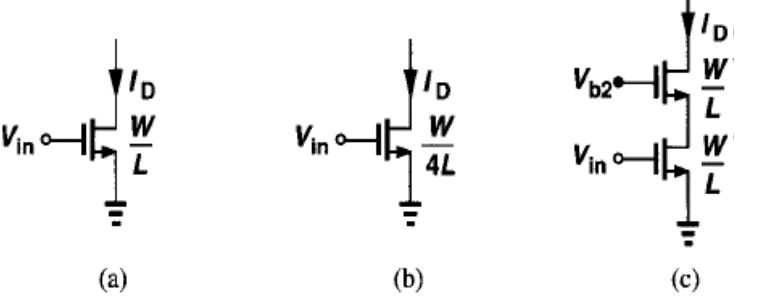
在这里插入图片描述

5.1.4 共源共栅电流源负载

共源共栅结构不一定起放大器的作用，这种结构还可以用来构成恒定电流源，高的输出阻抗提供一个接近理想的电流源，但这会损失电压余度。

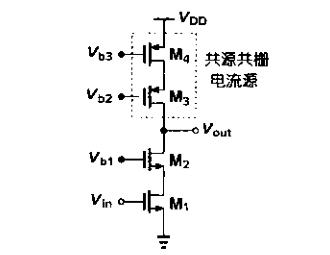
在这里插入图片描述
电流源变现出的输出阻抗 [ 1 + ( g m 3 + g m b 3 ) r 03 ] 04 + r 03 [ 1 + ( g _ { m 3 } + g _ { m b3 } ) r _ { 03 } ] _ { 04 } + r _ { 03 } [1+(gm3​+gmb3​)r03​]04​+r03​ 总的输出阻抗 R o u t = { [ 1 + ( g m 2 + g m b 2 ) r o 2 ] r o 1 + r o 2 } / / { [ 1 + ( g m 3 + g m b 3 ) r o 3 ] r o 4 + r o 3 } R _ { o u t } = \{ [ 1 + ( g _ { m 2 } + g _ { m b _ { 2 } } ) r _ { o 2 } ] r _ { o 1 } + r _ { o 2 } \} // \{ [ 1 + ( g _ { m 3 } + g _ { m b 3 } ) r _ { o3 } ] r _ { o4 } + r _ { o3 } \} Rout​={[1+(gm2​+gmb2​​)ro2​]ro1​+ro2​}//{[1+(gm3​+gmb3​)ro3​]ro4​+ro3​} 最大输出摆幅 V D D − ( V G S 1 − V T H 1 ) − ( V G S 2 − V T H 2 ) − ∣ V G S 3 − V T H 3 ∣ − ∣ V G S 4 − V T H 4 ∣ V _ { D D } – ( V _ { G S 1 } – V _ { T H 1 } ) – ( V _ { G S 2 } – V _ { T H 2 } ) – | V _ { G S 3 } – V _ { T H 3 } |- |V _ { G S 4 } – V _ { T H 4 } | VDD​−(VGS1​−VTH1​)−(VGS2​−VTH2​)−∣VGS3​−VTH3​∣−∣VGS4​−VTH4​∣ 输出摆幅大约等于VDD减去4个过驱动电压

5.1.5 屏蔽特性

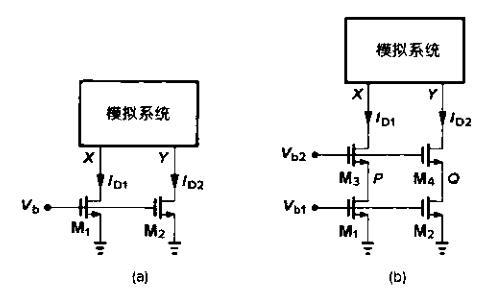
在这里插入图片描述
对图a有： I D 1 − I D 2 = 1 2 μ n C o x W L ( V b − V T H ) 2 ( λ Δ V ) I_{D1}-I_{D2}= \frac{1}{2}\mu _{n}C_{ox}\frac{W}{L}(V_{b}-V_{TH})^{2}(\lambda \Delta V) ID1​−ID2​=21​μn​Cox​LW​(Vb​−VTH​)2(λΔV) 对图b有： △ V P Q = △ V r o 1 [ 1 + ( g m 3 + g m b 3 ) r o 3 ] r O 1 + r O 3 ≈ △ V ( g m 3 + g m b 3 ) r o 3 △ V _ { PQ } = △ V \frac { r _ { o 1 } } { [ 1 + ( g _ { m 3 } + g m b 3 ) r o 3 ] r _ { O 1 } + r _ { O 3 } } \approx \frac { △V } { ( g _{m 3} + g _ { m b 3 } ) r _ {o 3 } } △VPQ​=△V[1+(gm3​+gmb3)ro3]rO1​+rO3​ro1​​≈(gm3​+gmb3​)ro3​△V​ 共源共栅使ID1与ID2的失配减少了 ( g m 3 + g m b 3 ) r o 3 ( g _ { m 3 } + g _ { m b 3 } ) r _ { o3 } (gm3​+gmb3​)ro3​倍，这在第5章电流镜中有重要应用

转自：https://blog.csdn.net/qq_42903635/article/details/131355004