目录
替代定理
在证明戴维南定理之前，我们必须先引入
替代定理
替代定理是对电路进行等效变换的一种形式，是用电压源或电流源来等效替代某条支路或部分电路，替代前后电路中各支路电压电流不发生变化。
简单用图形来表示就是这样的
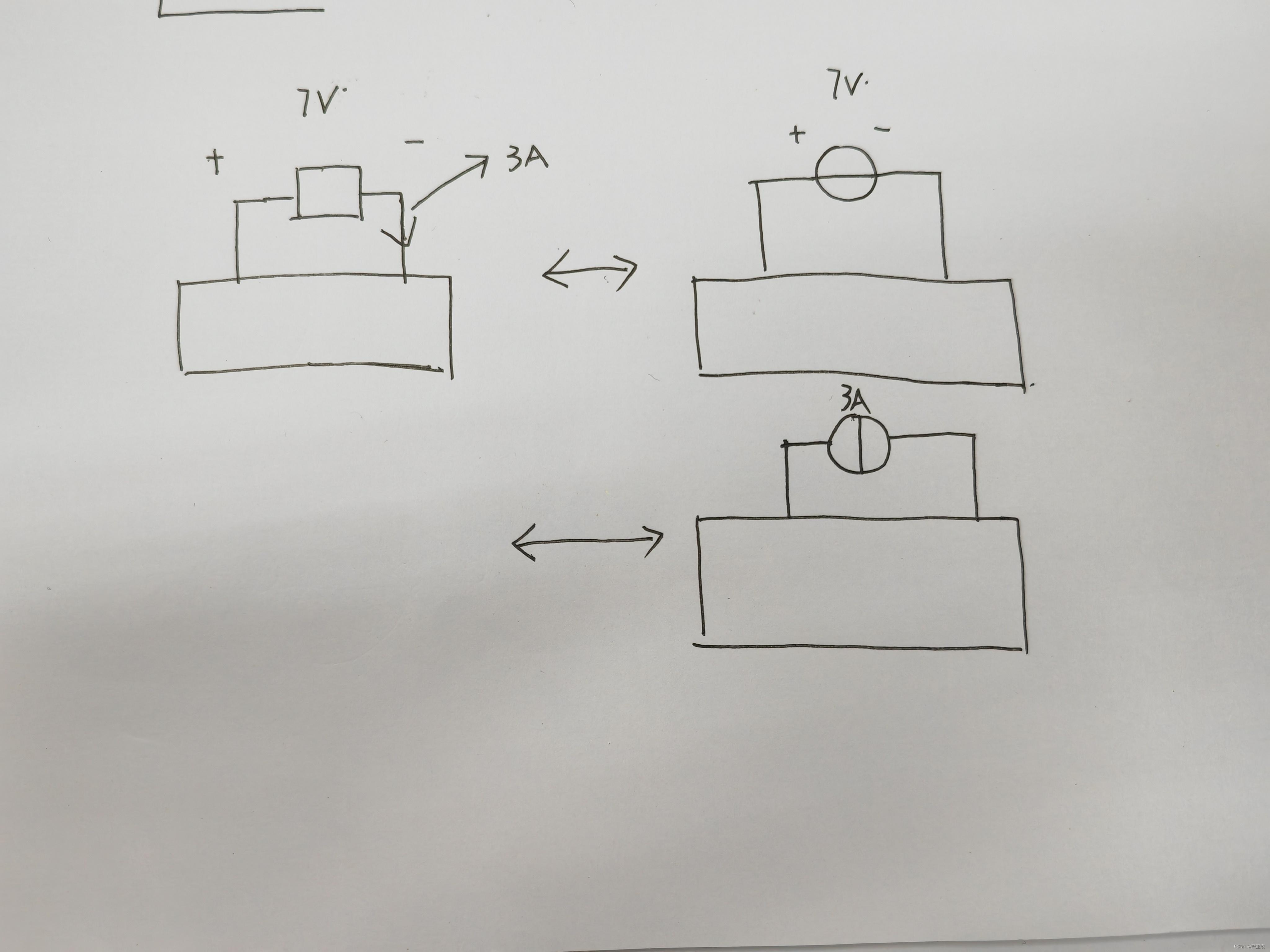
在下面方框以内电路结构不变
替代电路的应用较为广泛，它不仅适用于线性电路，也可推广至非线性电路分析。
定理的详细说明
替代定理（substitution theorem）
给定任意一个电路，假设某一条支路两端的电压为U，流经该支路的电流为I。
则该支路可以用一个电压为U的独立电压源替代，电压源的极性与原支路电压极性相同；
该支路也可以用一个电流为I的独立电流源替代，电流源的电流方向与流经原支路电流方向相同，替代后电路中各支路电压电流与替代前电路中相应的变量相等。
先用一个例子来说明替代定理。图 3.5.1（a）所示电路中，可求出ab两点间的电压为10V，由a点流入右边端口的电流是2A。那么，就可以用一个电流为2A的电流源（如图3.5.1（b））或一个电压为10V的电压源（如图3.5.1（c））来替代ab右边的一端口电路，替代前后7A电流源的端电压和2Ω电阻的电压、电流相等。
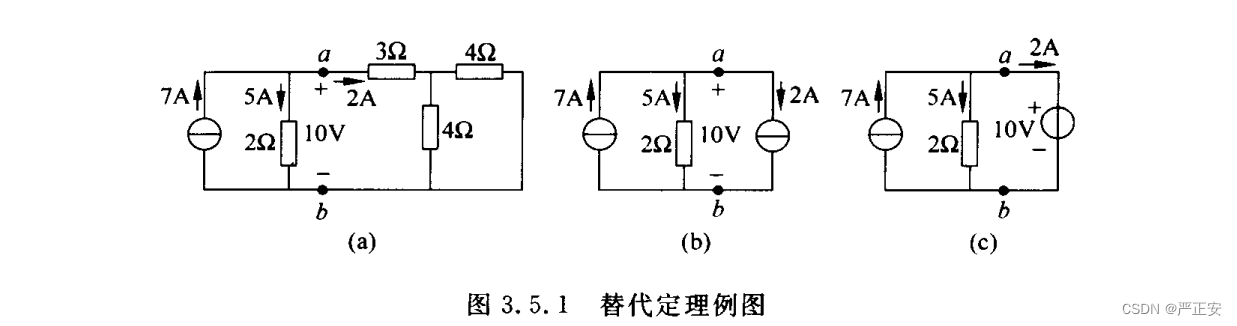
替代定理的证明
不失一般性，在图3.5.2（a）所示电路a—b右边支路中串接两个电压相等、极性相反的独立电压源，如图3.5.2（b）所示。令电压源的大小等于ab端口电压U，显然电压源的接入不会影响原电路（ab左边端口）中各支路电压、电流。图3.5.2（b）中c点和b点的电位相等，可将c和b两点短路，得到图3.5.2（c）所示的电路。这样做不会影响电路其他部分的电压和电流，从而定理得以证明。类似地，可以证明用电流源替代的正确性。
替代定理的应用
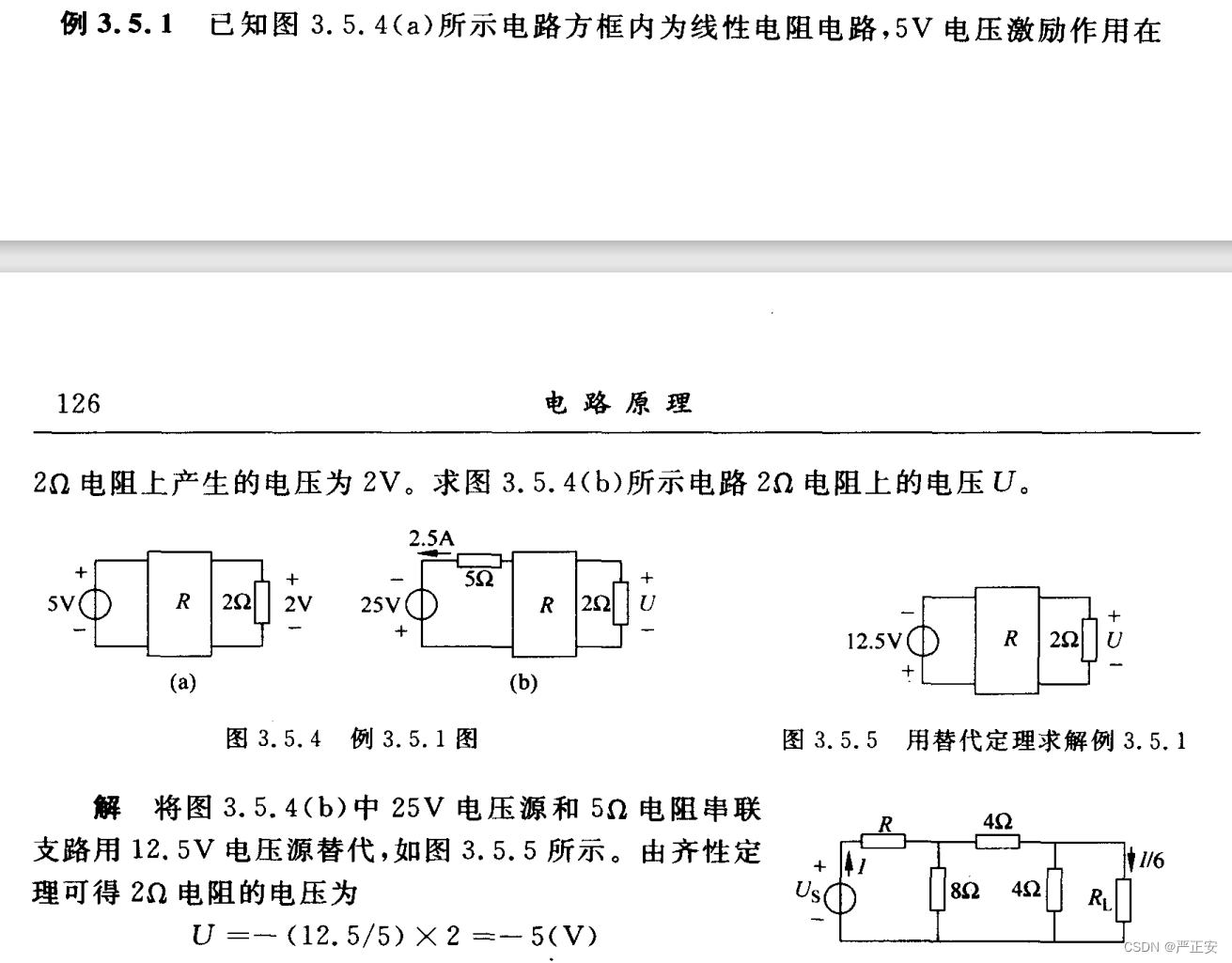
戴维南定理的证明
戴维南定理（Thevenin＇s theorem）
可描述如下。任意一个由线性电阻、线性受控源和独立电源组成的一端口电路（图3.6.1（a））对外部的作用都可以用一个理想电压源U。和电阻R的串联电路来等效（图3.6.1（b）），此理想电压源在数值上等于一端口电路在端口处的开路电压（open-circuit voltage）
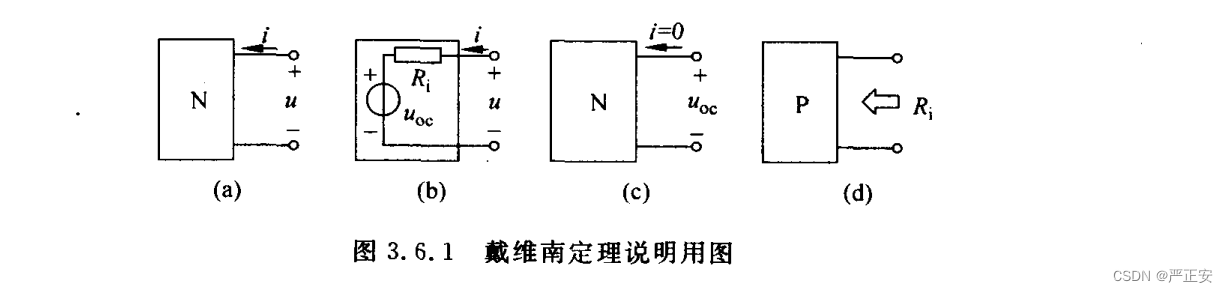
戴维南等效电路的概念
图3.6.1（b）
所示电压源和电阻串联电路被称为戴维南等效电路（Thevenin＇s equivalentcircuit）
戴维南等效电阻的概念
图3.6.1（d）
所示的电阻R，称为戴维南等效电阻（Thevenin＇s equivalent resistance）
戴维南定理的一般性证明
下面对戴维南定理做一般性证明
电路原理
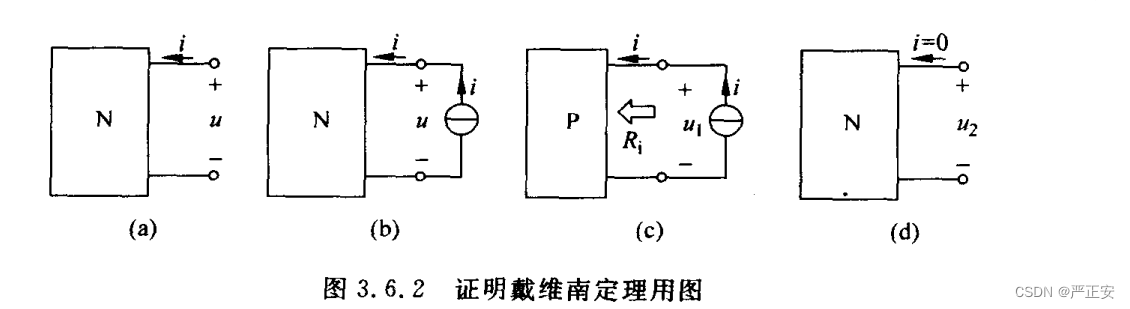
图3.6.2（a）所示一端口电路内部是含有电阻、独立电源和受控电源的线性电路，下面讨论端口电压、电流的关系。为了用电流i来表示端口电压u，在端口加一个电流源激励，如图3.6.2（b）所示
根据叠加定理，端口的电压
其中，电压
式中
电压
根据叠加定理，有
因此，无论端口内部电路结构多么复杂，端口上电压、电流可表示为式（3.6.1）所示的简单关系，也就是说可以将该一端口等效为一个电压源
当该一端口外接负载时，图3.6.1（a）所示电路和图3.6.1（b）所示电路对负载而言是相互等效的，如果将相同的负载接到这两个电路的端口上，则在负载上将得到相同的电压和电流。
戴维南等效电路包括一个电压源和一个电阻。电压源的电压是端口开路时的开路电压，可用节点电压法、回路电流法、叠加定理、简单电阻电路分析方法直接求得。戴维南等效电阻的求解方法将结合具体例子加以说明。
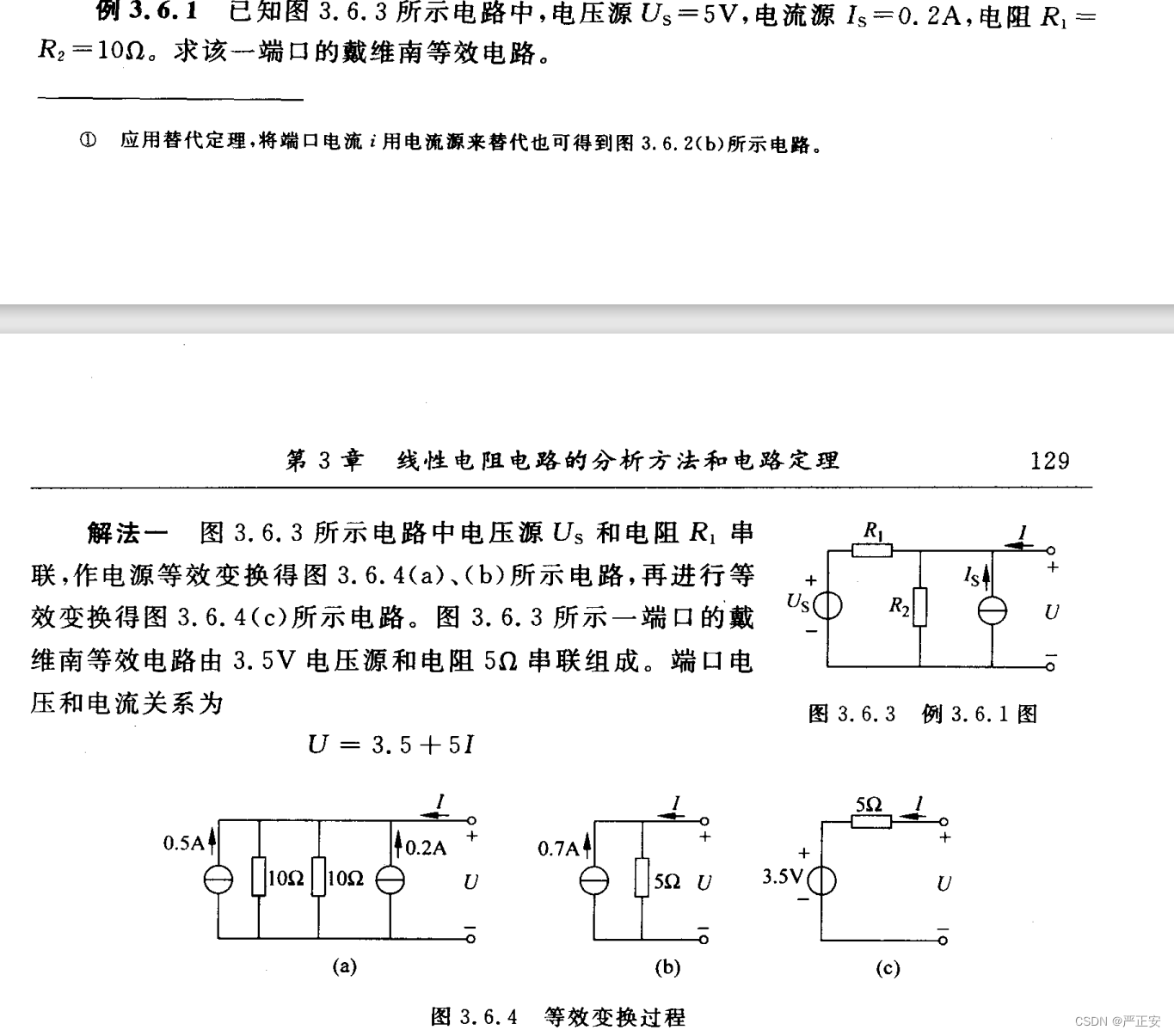
戴维南定理的应用
转自：
https://blog.csdn.net/m0_52555753/article/details/130254071