1.基尔霍夫第一定律-KCL定律,依据是电流连续性原理。通用公式为:
2.基尔霍夫第二定律-KVL定律,通用公式为:,必须选定电流参考方向,回路绕行方向。
3.
什么是混联电路
混联,是指既有串联又有并联的结构方式,在电路、机床、混合动力系统等中常用。其中电路即叫混联电路。方式为串联电路和并联电路。
混联电路的分析方法
首先明确电路各部分的连接方法,然后分析出局部电路电阻的变化对电路总电阻的影响,进而分析出电路总电流的变化,由总电流的变化分析各部分电压的变化,由各部分电压的变化分析局部电路上电流变化思路为:局部电阻变化→总电阻变化→总电流变化→各部分电压变化→局部电流变化。
分析总电阻变化时注意:
(1)电阻串联:其中之一变大,串联电路总电阻变大;其中之一变小,总电阻也变小。
(2)电阻并联:其中之一变大,并联电路总电阻变大;其中之一变小,总电阻也变小。
混联电路的分析与计算
一)节点法
该法是简化混联电阻电路最有效的且用得最多的一种方法。它采用四个步骤:
1.确定计算哪两端间的电阻。
2.找出电路中的独立节点(节点:三条或三条以上支路的连接点)。电路中有直接用导线连接的两点,应视为同一个点(即等电位点)。
3.把各节点、两端点竖直(或水平)排列。两端点位于最外层。
4.连接节点间、端点间和节点与端点间的电阻。连接两节点间、两端点间和节点与端点间的电阻时,不能穿过其他节点或端点。
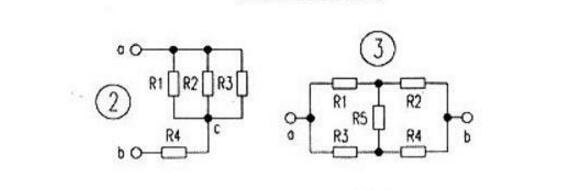
例:如图1电路中,已知R1=R2=R3=R4=6Ω,求电路中a、b间的电阻?
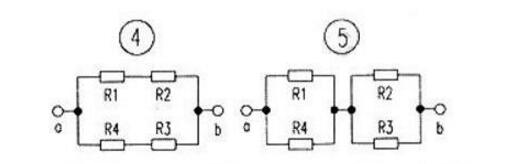
分析:利用节点法,就可将图l原电路等效为图2所示电路,由图2可知,R1、R2电阻与R3并联后,再与R4串联,即为a、b间的电阻Rab。
解:∵1/R123=1/R1+1/R2+1/R3=1/6十1/6+1/6=1/2
R123=2Ω
Rab=R123+R4=6Ω+2Ω=8Ω.

二)平衡电桥等效法
该法是简化具有平衡电器桥路最有效的一种方法。它利用电桥电路平衡时,桥支路可视为开路或短路的原理来实现将原混联电阻电路向串联并联电阻电路的等效变换。
电桥电路如图3所示,由电阻R1~R5构成的电路就是一个电桥电路。其中由电阻R5构成的支路,称为“桥支路”:由电阻R1一R4各自构成支路,称为“桥臂支路”,电阻R1~R4称为“桥臂电阻”。
电桥平衡时,桥支路可视为开路或短路,这是因为当桥支路的电流为零或桥支路两端电位相等时,电桥平衡。所以电桥平衡时,当桥支路的电流为零时,桥支路当然可视为开路(如图4):当桥支路两端电位相等时,桥支路当然可视为短路(如图5)。
怎样确定电桥电路是否平衡呢?在电桥电路中,当相对“桥臂电阻”乘积相等(或相邻“桥臂电阻”比值相等),则原电桥电路平衡(可推导)。
通过以上分析.利用本法化简带平衡电桥的混联电阻电路只用两个步骤:1、利用电桥电路平衡条件确定电桥式混联电阻电路是否平衡。2、如果原电路是平衡的,对桥支路进行开路或短路的等效处理。
例:如图3所示电路中,已知R1=20Ω,R2=40Ω,R3=60Ω,R4=30Ω,R5=50Ω,求电路中a、b间的电阻?
分析:先对原电桥电路进行平衡判断,如果原电路是平衡的.对桥支路进行开路等效处理。按图4电路进行计算(当然也可按图5处理)。由图4电路可知,电阻R1与R2,电阻:R3与R4先串联,然后再并联即为a、b间的电阻。
解:∵R1·R3=20×60=1200(Ω)
R2·R4=40×30=1200(Ω)
R1·R3=R2·R4
∴该电桥电路平衡
原电桥电路(图3)等效为图4电路
R12=Rl+R2=201Ω+40Ω=60Ω
R34=R3+R4=60Ω+30Ω=90Ω
Rab=R12·R34/(R12+R34)=(60×90)/(60+90)=36(Ω)
三)电阻网络等效互换法
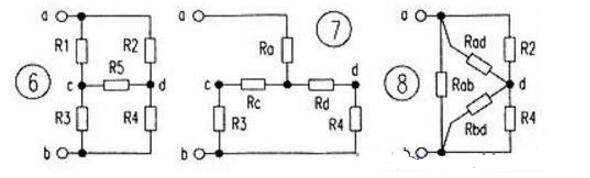
该法是简化具有不平衡电桥电路最有效的一种方法。它利用△一Y电阻网络等效互换来实现将原混联电阻电路向串联并联电阻电路的等效变换。如图6所示,由电阻R1、R2、R5构成的电路就是一个“△”电阻网络。由电阻R1、。R3、R5构成的电路就是一个“Y”电阻网络。
如何实现△一Y电阻网络等效互换呢?如果原电路中有“△”电阻网络,那么可转化为“Y”电阻网络来实现不平衡电桥的混联电阻电路向串联并联电阻电路的等效变换,常将这种等效变换称为“△一Y”(图6转化为图7)。但转化后的“Y”电阻网络中的电阻Ra、Rc、Rd与原电路中“△”电阻网络中的电阻Rl、R2、R5要遵循公式:Ra=(Rl·R2)/(R1+R2+R5);Rc=(R1·R5)/(R1+R2+R5);Rd=(R5·R2)/(Rl+R2+R5)。(可推导)如果原电路中有“Y”电阻网络,那么可转化为“Y一△”电阻网络来实现不平衡电桥电阻电路向串联并联电阻电路的等效变换,常将这种等效变换称为“Y一△”(图6转化为图8)。但转化后的“△”电阻网络中的电阻Rab、Rad、Rbd与原电路中“Y”电阻网络中的电阻Rl、R3、R5要遵循公式:Rab=(Rl·R3+Rl·R5+R3·R5)/R5:Rad=(R1·R3+R1·R5+R3·R5)/R3:Rbd=(Rl·R3+R1·R5+R3·R5)/Rl。(可推导)通过以上分析,利用本法化简不平衡电桥的混联电阻电路采用三个步骤:1.利用电桥电路平衡条件确定电桥式混联电阻电路是否平衡。2.如果原电路是不平衡的。对原电路中的“△”电阻网络或“Y”电阻网络进行“△一Y”或“Y一△”的等效变换。3.将变换后电阻的阻值按相应公式算出。
例:如图6所示电路中,已知R1=2Ω,R2=2Ω,R3=2Ω,R4=1Ω,R5=1Ω,求电路中a、b间的电阻?
分析:先对原电桥电路进行是否平衡判断,如果原电路电桥平衡的,按“平衡电桥等效法”处理,如果原电桥电路不平衡的,按“电阻网络等效互换法”处理。据已知原电桥电路不平衡,故图6按图7电路进行等效处理(当然也可按图8处理)。由图7电路可知,电阻R3与Re,电阻R4与Rd先串联,然后再并联,最后再与Ra串联即为a、b间的电阻。
解:∵R1·R4=2xl=2(Ω)R2·R3=2×2=4(Ω)Rl·R4《R2·R3∴该电桥电路不平衡原电桥电路(图6)等效为图7电路即对原电路进行“△一Y”
Ra=(R1·R2)/(R1+R2+R5):(2×2)/(2+2+1)=0.8(Ω)Rc=(R1·R5)/(R1+R2+R5)=(2×1)/(2+2+1)=0.4(Ω)Rd=(R5·R2)/(R1+R2十R5)=(2×1)/(2+2+1)=0.4(Ω)Rab=0.8+(2.4×1.4)/(2.4+1.4)=1.68(Ω)在简化无源混联电阻电路时,首先要认真观祭电路结构,想想采用哪种方法更简单,其次要认识到上述三种简化法不是孤立的,而是辩证统一的。在实际电路中,往往可能用到两种或两种以上的方法,这需要读者朋友认真分析了。
简单混联电路的计算
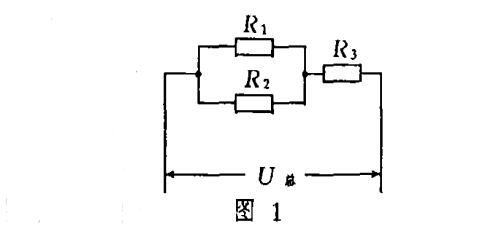
例1:如图1,电源电压是16V,R.一20Q,R2—30Q,R3—20Q,求:电路中的总电阻;R。消耗的功率;1分钟内电流在电路中产生的总热量。
解:由图可知R与R。并联后与R。串联
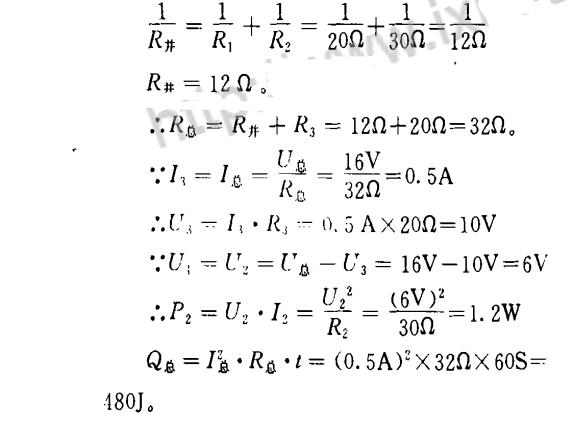
答:电路中的总电阻是32Q,R。消耗的功率是1.2W,1分钟内电流在电路中产生的总热量是480j。
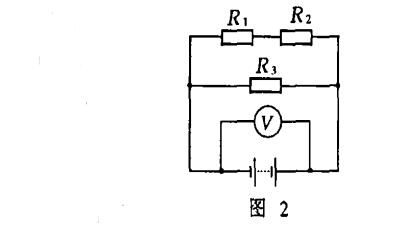
例2如图2,电压表的示数是12V,R一20Q,R2—20Q,R3—40Q,求:电路中的总电阻;电路中消耗的总功率;半分钟内电流在R上消耗的电功。
解:由题意得

答:电路中的总电阻是2012;电路中消耗的总功率是7.2W;半分钟内电流在R上消耗的电功是54J。
无法直接用串联和并联电路的规律求出整个电路的电阻时,称之为复杂电路。
电动势的方向:通常规定从负极通过电源内部指向正极的方向是电动势的方向,即与电源两端电压的方向相反。
理想电压bai源与理想电流源之间不可以进行等效变换;
实际电源可以模拟为理想电压源与内阻串联的形式,也可以模拟为理想电流源与内阻并联的形式。这两种形式之间可以等效变换。
带上负荷,公式应该是:P=U2/ (R负荷+R线路),线路的电阻和负荷的电阻串联
而U=U负荷 + U线路
串联电路里,电阻和分电压成正比,所以,线路电阻越大,分得电压越高,当然损耗越大。
解析:叠加定理可表述为:在线性电路中,任一支路的电压与电bai流,都是各个独立源单独作用下,在该支路中产生的电压与电流的代数之和。
从定义看,此定理,只能用在线性一次关系式电路里,而功率是2次的关系式,因为功率与电压、电流的关系不是相加(叠加)关系,而是平方关系。
对于线性非时变电路,虽然不能直接使用叠加定理来计算,但可以使用叠加定理计算出电阻上的电流I或者电压U,再根据P=I²R或者P=U²/R,就可以计算出电阻上的功率,所以,在求电阻功率时,不是不能使用叠加定理,而是不能把功率直接进行叠加。


转自:https://blog.csdn.net/shenwansangz/article/details/113857790
